We will give a brief summary of the axioms of one of the later
versions of Barwisean situation theory,
without much motivation and explanation, mainly to refer to them
later.
For a complete discussion, see barsit.
Axiom 3.1
Every relation is the major constituent of some basic infon, and
everything is a minor constituent of some basic infon.
Axiom 3.2
If
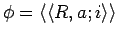
and
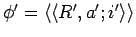
are basic
infons, then
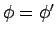
iff
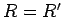
,
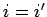
and
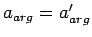
for each argument
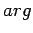
of
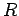
.
Axiom 3.3
Given an
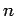
-ary relation
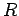
and an appropriate sequence
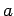
of
arguments for
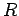
, either
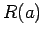
or
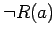
, but not both.
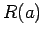
iff
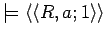
;
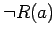
iff
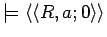
.
So far we can only talk about basic infons. Axiom 2 states under which
circumstances we will consider basic infons identical, namely when
they are identical item by item. However, infons are supposed to
capture information, so they may be informational equivalent,
although they are not identical item by item. Furthermore, given two
basic infons, one might be stronger than the other, so that one infon
is entailed by the other.
Axiom 3.4
Let
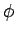
,
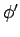
,
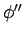
be infons. Then
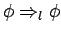
and
if
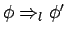
and
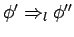
then
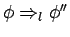
.
If
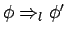
and
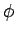
is a fact, then so is
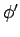
.
Axiom 3.5
Let
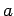
and
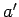
be appropriate assignments for
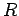
, and
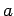
is a
sub-assignment of
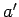
. For
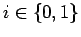
, let
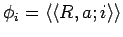
and let
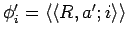
. Then
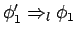
and
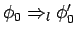
.
Axiom 3.6
Every set of infons
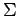
has a least upper bound (concerning
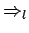
)
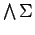
and a greatest lower bound
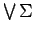
.
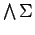
is a fact iff each infon in
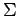
is a
fact,
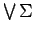
is a fact, iff some infon in
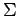
is a fact.
Axiom 3.7
The basic infons
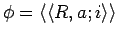
and
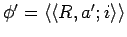
are compatible iff
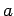
and
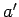
are compatible as functions. Then
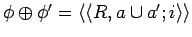
.
Now, for the first time, we will consider situations. A situation is
``a part of reality that can be comprehended as a whole in its own
right - one that interacts with other things.''barsit
They relate to other things of the world in the sense, that they stand
in relation to other things, or have properties.
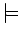 is a binary relation, holding between situations and
infons.
is a binary relation, holding between situations and
infons.
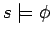 means ``
means ``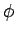 holds in the situation
holds in the situation 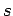 ''.
''.
Axiom 3.8
An infon
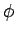
is a fact iff there is a situation
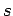
such that
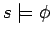
.
Axiom 3.9
A situation
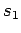
is a part of a situation
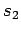
,
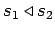
, if
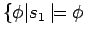
and
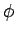
is a basic infon
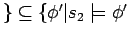
and
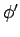
is a basic infon
. If
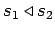
and
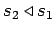
, then
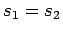
.
Therefore the part-of relation between situation is a partial
ordering.
Barwise takes the axioms now a step further and defined some kind of
interpretation for situations by stating the relation between sets and
situations.
Axiom 3.10
Every set
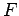
of facts determines a smallest situation
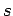
such that
for every
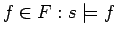
.
Axiom 3.11
Every set is the set of constituents of at least one situation.
The last axiom brings in models of situations.
leechuck
2005-04-19
![]() is a binary relation, holding between situations and
infons.
is a binary relation, holding between situations and
infons.
![]() means ``
means ``![]() holds in the situation
holds in the situation ![]() ''.
''.