The difference between situations and situoids

Situoids are basic entities, while situations depend on situoids. According to herre3, situoids ``are the most complex integrated wholes of the world, and they have the highest degree of independence.'' Situoids do not need other entities in order to exist. Situoids exist in time and space. Every situoid is framed by a chronoid and a topoid. Therefore, situoids extend in time. Two other properties of situoids are mentioned. Situoids have to be coherent, and, again, comprehensible as a whole. An association relation between situoids and certain universals is supposed to assure this notion.

Definition 5.10 (Situoid)   A situoid is an entity that does not need other entities in order to exist. Situoids are coherent and spatially and temporally connected. They have a temporal and spatial extent. $Situoid$ is the class of all situoids.

This is a very preliminary definition, and still needs some refinement. The main purpose for this definition is that we can refer to the class $Situoid$ later.

We can postulate the first axiom about situoids.

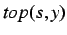
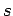
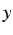
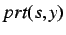
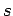
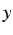
Axiom 5.9   Every situoid is framed by a chronoid and a topoid. The relation $top(s,y)$ has the meaning ``the situoid $s$ occupies the topoid $y$'' and $prt(s,y)$ has the meaning ``the situoid $s$ is framed by the chronoid $y$''. Then

$$\forall x (Situoid(x) \rightarrow \exists t \exists s (Topoid(s) \land Chronoid(t) \land top(x,s) \land prt(x,t)))$$

Situations are endurants. They are projections of situoids on time-boundaries of their framing chronoid. herre3 states that situations have to fulfill certain principles of unity and must be comprehensible as a whole, which is again assured using a relation between situations and universals. We will not pose this restriction, but merely state, that every projection of a situoid on a time-boundary of its framing chronoid is a situation.

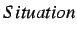
Definition 5.11 (Situation)   A situation is the projection of a situoid on a boundary of its framing chronoid. $Situation$ is the class of all situations.

Again, this is a preliminary definition, that needs refinement. But, contrary to our definition of situoids, this definition is much closer to our final version. Because situations depend existentially on situoids, some of their features and properties can be deduced from the properties of situoids.