Axioms of situoid theory

Before we can advance any further and show some of the results and further properties of this situoid theory, we will have to formalize our work done so far. The best way to do this is to write down axioms. Our theory will be far from complete at this stage, but to proceed we will need some axioms.

Our first axioms state that there is a state of affairs and there is a situoid and there is an infon.

Axiom 5.10  

$$\exists x (SOA(x))$$

$$\exists x (Situoid(x))$$

$$\exists x (Infon(x))$$

The next axiom concern the $\models$-relation and asserts that situoids are not incoherent.

Axiom 5.11   For all situoids $s$ and infons $\phi=\langle\langle R,a;p \rangle\rangle$, the following is true: If $s \models \phi$, then $s \not\models \bar{\phi}$, where $\bar{\phi} = \langle\langle R,a;1-p \rangle\rangle$.

Now we can define an ordering relation on situoids. All infons that obtain in a situoid $s_1$ that is part of another situoid $s_2$ also obtain in $s_2$.

Axiom 5.12  

$$\forall s_1 \forall s_2 (s_1 \leq s_2 \rightarrow (\forall \phi (s_1 \models \phi \rightarrow s_2 \models \phi)))$$

Now we can state that two situoids are identical, if and only if they are part of each other, and their framing chronoid and topoids are identical. The reason we have to assert the identity of the framing chronoid and topoid are ontological in nature: It will be possible to descibe two different situoids, say, two different marathons, with exactly the same information. So both situoids are informationally equivalent, but present at different space-time coordinates.

Axiom 5.13  

$$\begin{split}s_1=s_2 \iff s_1 \leq s_2 \land s_2 \leq s_1\lan... ...land prt(s_1,c_1) \land prt(s_2,c_2) \land c_1=c_2) \end{split}$$

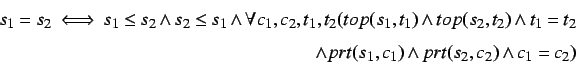Let us emphasize at this point, that the identity of the situoids framing chronoid and topoid may not be a sufficient criterion for identity. This is due to granularity considerations. We may descibe some scene from a birds-eye view, with only the basic information present, but we could descibe the same scene very detailed, adding waste amounts of information. As an example, consider a marathon. From a birds-eye view, the duration of the marathon, the position of the runners and maybe the names of the runners are the facts of this situoid. On the other hand, there is another situoid framed by the same topoid and the same chronoid, but with much more information available: The mood of the runners, the scenery, the altitude of the track, the weather, et cetera. We will consider this indeed a different situoid, and although both situoids are framed by the same chronoid and topoid, they are not identical. Therefore, situoids are not only spatio-temporal parts of the world, but also granular parts.

This is only the very beginning of a theory of situoids, but before we proceed, we will turn back out attention to infons.