Next: Hyperset-based model theory Up: Models for situations Previous: Models for situations Contents
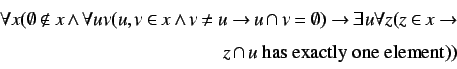 |
A set is well-founded, if it does not have an infinite descending membership sequence, otherwise non-well-founded. This notion is quite old, and well-founded as well as non-well-founded sets have been studied for decades. The notion has been introduced 1917 by Dmitry Mirimanov. Although there have been a number of attempts to replace the foundation axiom of ZFC, there has not been a major breakthrough in applications for non-well-founded sets until the revolutionary work of Peter Aczel in 1988aczset. Before Aczel, there have been a few anti-foundation axioms, due to M. Forti and F. Honsell, P. Finsler, or Dana Scott. The axiom AFA by Forti and Honsell has been adopted by Aczel.
Peter Aczel used a graph representation of sets, where an arrow
between the nodes ![]() and
and ![]() denotes the membership relation
denotes the membership relation 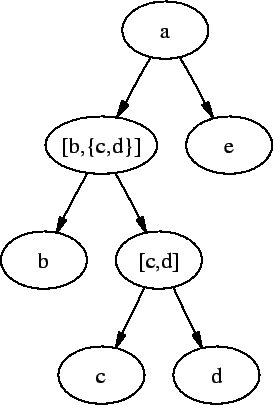 . A set in graph representation is called well-founded, if it does
not have any cycles or infinite descending branches. Figure 5.7
shows the simple well-founded set
. A set in graph representation is called well-founded, if it does
not have any cycles or infinite descending branches. Figure 5.7
shows the simple well-founded set ![]() . The more complex set
. The more complex set
![]() is show in figure 5.8.
is show in figure 5.8.
The anti-foundation axiom AFA states, that every set, well-founded or
not, pictures a unique set. Removing the foundation axiom from ZFC and
adding AFA instead leads to the hyperset theory ZFC/AFA. Now, the
so-called Quine atom ![]() can be pictured by a graph, as can be
seen in figure 5.9.
However, the same unique set can be pictured by many different graphs,
as can be seen in figure 5.10.
can be pictured by a graph, as can be
seen in figure 5.9.
However, the same unique set can be pictured by many different graphs,
as can be seen in figure 5.10.
Aczel stated, that there has to be a fundamental structural difference between graphs to model different sets. He introduced the notion of a bisimulation between two graphs.
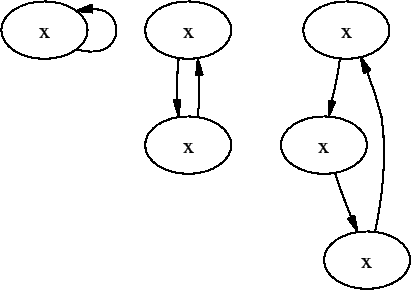 with point
with point  there exists an
edge
there exists an
edge
 such that
such that leechuck 2005-04-19