Next: Situation Theory Up: Situation Theories Previous: Situation Theories Contents
Properties subject to change are called fluents.
Changes from one situation to another are modeled using a function,
![]() . The atomic
predicate
. The atomic
predicate
![]() is true, if the fluent
is true, if the fluent ![]() is true in the
situation
is true in the
situation ![]() .
.
Actions are described by stating their effects. Therefore effect axioms have to be stated, describing the properties of a situation that results from doing some action. However, this is not enough. One also has to state axioms describing a situation after not performing an action. Those are called frame axioms. Frame axioms have to be stated for every fluent and action. Another solution is to use a successor-state axiom. This axioms states, that a fluent is true after some action, if an action made it true or it has been true and no action made it false.
This is a very weak theory of situations. The world consists of a series of snapshots, that are complete on its own. There is no development within a situation, since they do not have a duration. We shall therefore turn our attention to a more complex theory of situations.
But first, let us consider an example. We want to open a bottle of beer, smell
the beer
and after that we drink the beer. So the fluents we have to
consider are ![]() and
and ![]() , the actions will be
, the actions will be ![]() and
and
![]() .
.
We start off with the beer closed and not empty.
Now we want to perform the action of opening the beer, ending up in a new situation.
After we finished this ritual, we finally want to drink the beer, ending up in a new situation.
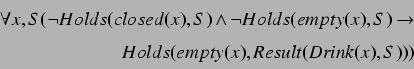 |
leechuck 2005-04-19