next up previous contents index
Nächste Seite: Beweis des Satzes 1 Aufwärts: Rot-Schwarz Baeume Vorherige Seite: Rot-Schwarz Baeume   Inhalt   Index

Definition und Eigenschaften

Definition 4.1: Ein Rot-Schwarz Baum ist ein regulaerer binaerer Baum, der folgende Bedingungen erfuellt[Cormen][Booth]:

  1. Jeder Knoten ist entweder rot oder schwarz.
  2. Jeder einfache Pfad von der Wurzel bis zu einem externen Knoten enthaelt genau die gleiche Anzahl von schwarzen Knoten.
  3. Jeder rote Knoten hat nur schwarze Nachbarn.
  4. Jeder externe Knoten ist schwarz.
Definition 4.2: Ein rot-schwarzer Suchbaum ist ein Rot-Schwarz Baum, der auch ein binaerer Suchbaum ist. [Cormen]

Aus den Bedingungen 1-4 folgt die wichtigste Eigenschaft eines Rot-Schwarz Suchbaumes, die wir in diesem Satz formulieren:

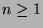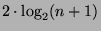Satz 1: Fuer alle \( n\geq 1 \) hat jeder Rot-Schwarz-Baum mit n Knoten eine maximale Hoehe von \( 2\cdot \log _{2}(n+1) \) ([Cormen] Seite 264).


root 2000-01-25