Categories of GOL

Figure 4.3: Hierarchy of Categories in GOL

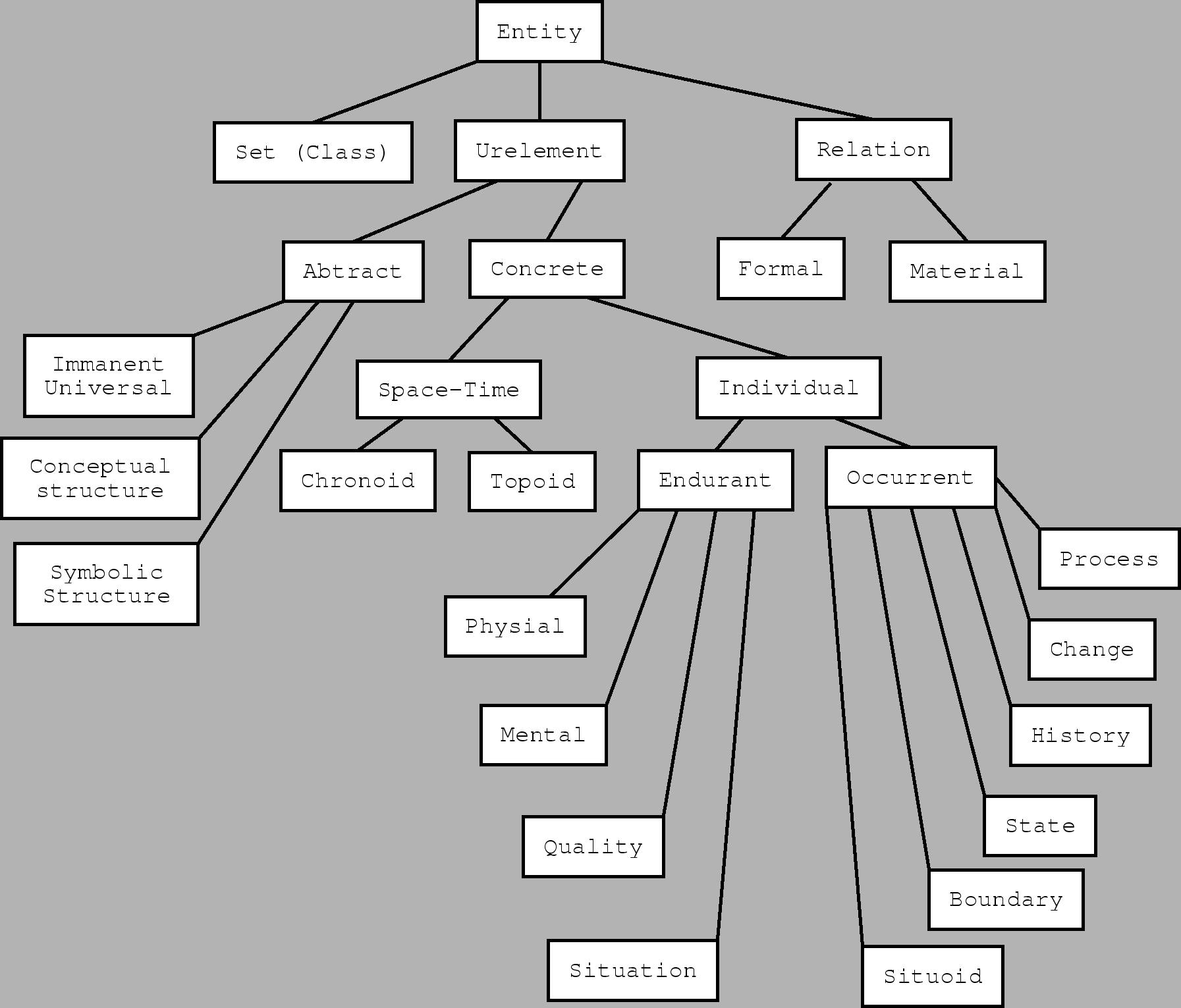Figure 4.3 shows the categories that are used in the GFO. Categories are collections of entities with a certain intension. If an entity is an instance of a certain category, then it has certain properties due to membership in that category. Let $a$ be an entity, and $X$ a category. We will write $a::X$ if $a$ is an instance of $X$. As usual, we can also write $a \in X$ if we mean, that $a$ is a member of the set $X$. However, intensionality is lost in the use of sets. Still, there is some relation between sets and categories:

Definition 4.1 (Extension of a category)   The extension of a category $C$ is the set $X=Ex(C)=\{x\vert x::C\}$.

A category is any of the broadest classes of ``things'', where ``thing'' here means anything that can be discussed and cannot be reduced to any other class. For example taking ``physical object'' as a category implies that physical object-hood cannot be reduced or expressed in any other terms, such as a bundle of properties as in section 4.1.2.

The GOL-categories that are of concern to this thesis are the categories of situation, situoid, and relations to some degree, as they are needed to build up facts. We also need to understand the concept of time and space in GOL, as well as the concept of a universal.