In GOL, time is divided in two basic entities: time boundaries and
chronoids. Chronoids are time intervals, and they always have a
duration. Time boundaries depend on chronoids: A chronoid has exactly
two time boundaries, a left and a right time boundary. We denote
chronoids with 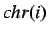 , meaning
, meaning 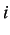 is a chronoid, and time-boundaries
with
is a chronoid, and time-boundaries
with 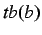 , meaning
, meaning 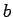 is a time boundary.
is a time boundary.
We use the relations:
-
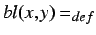
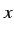 is left boundary of the chronoid
is left boundary of the chronoid 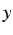
-
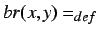
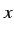 is right boundary of the chronoid
is right boundary of the chronoid 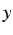
-
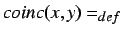 the time boundaries
the time boundaries 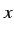 and
and 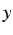 coincide
coincide
Defined is
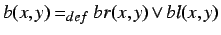 .
.
Let us view the axioms of this theory as in stenzel1.
The first axiom asserts the existence of a chronoid.
The second axiom asserts the uniqueness of the left and right boundary
of a chronoid.
The next axiom states that time boundaries and chronoids are disjunct.
The next axiom asserts that time is infinite: Every left boundary of a
chronoid coincides with the right boundary of another chronoid, and
vice versa.
Chronoids may have internal structure.
The last axiom asserts the linearity of time.
This theory of time and the theory introduced by allen1, using
only one relation, the relation 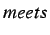 , are equivalent
, are equivalent![[*]](/usr/share/latex2html/icons/footnote.png) , as shown in stenzel1. Sometimes this model
of time is called the ``glass continuum''.
, as shown in stenzel1. Sometimes this model
of time is called the ``glass continuum''.
leechuck
2005-04-19
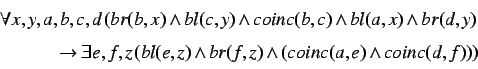

![]() , are equivalent
, are equivalent![]() , as shown in stenzel1. Sometimes this model
of time is called the ``glass continuum''.
, as shown in stenzel1. Sometimes this model
of time is called the ``glass continuum''.