Next: Are situations part of Up: Situations Previous: Situations Contents
Let us remember our definition for situations.
Situations exist at time boundaries. There is a function
![]() , where
, where ![]() is the set of all time
boundaries.
is the set of all time
boundaries.
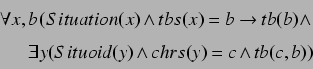 |
We can now define the relation, first mentioned in section
5.2.9, that a situation ![]() is part of a situoid
is part of a situoid ![]() .
.
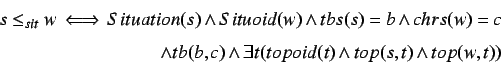 |
We define the supports relation from section 5.2.2 for situations as follows.
Timed infons do not make sense in situations, as situations exist at
precisely one point in time, a single time boundary, and the states of
affairs that correspond to the obtaining infons have to exist at the
same point in time. This does not mean, that the entities
participating in the states of affairs have to exist at
time-boundaries, too. As an example, consider the state of affairs
``The process ![]() 's being earlier than the process
's being earlier than the process ![]() ''.
''.
As we did for situoids, we can now define another, basic part of relation.
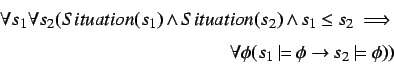 |
And also, two situations are identical, if and only if the same infons obtain in them, that is, if they are part of each other. Again, this is insufficient. They also have to exist at the same time boundary, and they have to be a situational part of the same situoid.
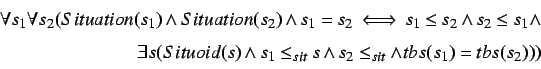 |
We extend the function ![]() , taking situoids into sets, to accept
situations as its arguments.
, taking situoids into sets, to accept
situations as its arguments.
Again, the same as for situoids, we do not want to permit empty situations.
Now we said that situations are comprehensible entities. Some of the axioms of section 5.2.8 have to be adapted and applied to situations. The first important condition is, that every situations has to be the instance of at least one universal.
The last axiom needed for situations to be comprehensible entities is the following:
leechuck 2005-04-19