Jon Barwise showed in barwise1 how to introduce modality into
situation theory, while keeping a strictly realistic point of view. We
will show how this is done and how to incorporate his approach in our
framework.
Definition 6.1 (Classification, Boolean Classification)
A classification
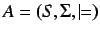
is a set of situoids or
situations
, a set of infons
and the relation
.
A Boolean classification
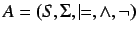 is a
classification together with
is a
classification together with 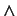 and
and 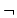 , defined on infons,
and satisfying the following:
, defined on infons,
and satisfying the following:
Barwise used Gentzen-type sequents to model information.
The following propositions about sequents hold, just as for classical
sequent calculus, such as LK gentzen1.
Theorem 6.1
Let 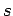 be any situation or situoid.
be any situation or situoid.
-
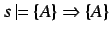 (Identity)
(Identity)
- If
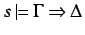 then
then
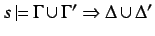 (Weakening)
(Weakening)
- If
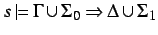 for each partition
for each partition
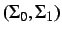 of some set of
infons
of some set of
infons 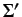 , then
, then
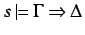 (Global Cut)
(Global Cut)
- If
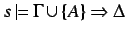 , then
, then
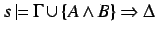 and also
and also
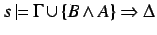 (
(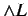 )
)
- If
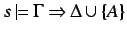 and
and
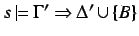 then
then
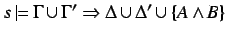 (
(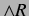 )
)
- If
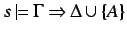 then
then
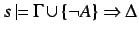 (
( )
)
- If
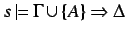 then
then
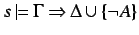 (
(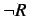 )
)
Proof.
- To show is that if
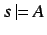 then
then
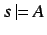 , that is
, that is
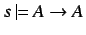
![[*]](/usr/share/latex2html/icons/footnote.png) , which is a tautology.
, which is a tautology.
- For all
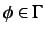 ,
,
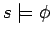 , and for some
, and for some
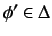 ,
,
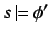 . To show is, if for all
. To show is, if for all

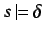 , there is some
, there is some
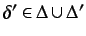 with
with
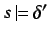 . If
this was not the case, there would be no such
. If
this was not the case, there would be no such
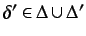 , but a
, but a
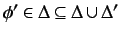 , which is a contradiction.
, which is a contradiction.
- Proof can be found in barwise1.
- To show is, that if
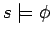 for all
for all
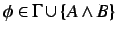 then there is some
then there is some
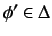 so that
so that
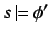 . If this was not the case, then
. If this was not the case, then
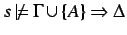 which is a
contradiction. The proof is similar for the other direction.
which is a
contradiction. The proof is similar for the other direction.
- Given is
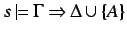 and
and
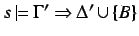 . If
. If
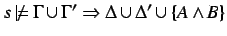 , then for all
, then for all
 but for no
but for no
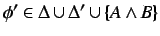
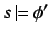 . There is some
. There is some
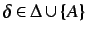 and
some
and
some
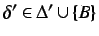 with
with
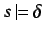 and
and
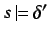 . If
. If
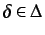 then there is a
then there is a
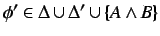 with
with
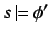 which is a contradiction. The same holds for
which is a contradiction. The same holds for
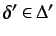 . So
. So 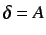 and
and 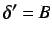 and
and
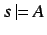 and
and
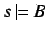 . But then
. But then
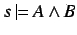 , which is again a
contradiction.
, which is again a
contradiction.
- Given is
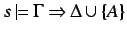 . Assume
. Assume
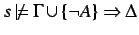 , then for all
, then for all
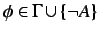
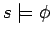 , but for no
, but for no
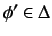
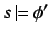 , while
there is a
, while
there is a
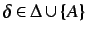 with
with
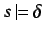 . If
. If
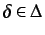 we have a contradiction, so
we have a contradiction, so
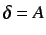 and
and
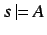 , while at the same time
, while at the same time
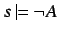 , which is a contradiction.
, which is a contradiction.
- The proof is similar to the previous.
<1.5em -
height0.75em width0.5em depth0.25em
These rules taken as inference rules are complete barwise1.
Barwise introduces information contexts, also called local logics.
Definition 6.3 (Information context, Boolean information context)
An information context
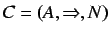
is a classification
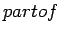
, a binary relation
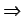
relating sets of infons and a
set
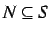
of situations
![[*]](/usr/share/latex2html/icons/footnote.png)
called normal
situations.
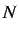
is closed under identity, weakening and
global cut, and for all
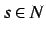
and all
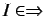
:
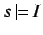
.
A boolean information context is one where 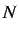 is also closed under
the rules (
is also closed under
the rules (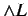 ), (
), (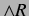 ), (
), (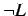 ) and (
) and (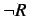 ).
).
The idea is that 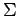 , the set of infons from
, the set of infons from 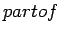 , represents the
relevant issues,
, represents the
relevant issues,
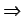 the information present, while
the information present, while 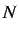 are
the situations supporting this information. They may, but do not have
to be all the situations.
are
the situations supporting this information. They may, but do not have
to be all the situations.
Barwise continues by introducing possible worlds, which he calls
``states'' to distinguish them from Lewisian possible worlds
in lewis1. We will call them possible worlds anyway.
Now it can be shown, that every normal situation is possible, and if
the information context is sound, every situation is possible as well
as if the information context is complete, then every possible world
is realized by some normal situation.
Before we can introduce modalities, we need one more definition,
defining what is meant by one information context being less
informative than another.
Now modalities can be introduced.
Definition 6.6 (Informational modal framework)
An informational modal framework
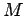
is a classification
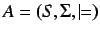
, and an
information context
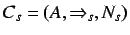
for each situation
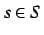
,
satisfying the condition: If
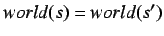
then
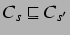
and
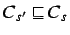
. All
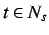
are called
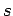
-normal. All worlds possible relative to
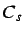
are
called
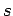
-possible.
Now propositions are taken as sets of possible worlds. It follows the
final definition in barwise1, modified to fit our terminology.
With these definition, Barwise shows in barwise1 several
theorems known from modal logics, and we will name the more important
ones.
A proposition is valid in the informational modal framework 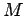 ,
written
,
written
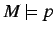 iff
iff
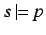 for all situations
for all situations
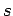 in
in 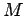 . Then for any modal information frame
. Then for any modal information frame 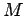 and any
propositions
and any
propositions 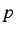 and
and 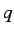 ,
,
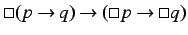 ,
,
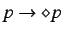 and
and
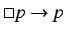 are valid.
are valid.
Several other theorems are proven in barwise1, and all of them
can be adapted to the framework of situoids and situation of this
thesis. Therefore, this may be an elegant way of introducing
modalities in the ontology of GOL.
leechuck
2005-04-19
![]() is a
classification together with
is a
classification together with ![]() and
and ![]() , defined on infons,
and satisfying the following:
, defined on infons,
and satisfying the following:
![]() holds of a situation (or
situoid)
holds of a situation (or
situoid) ![]() ,
,
![]() , if the following is true: If
, if the following is true: If
![]() for all
for all
![]() , then
, then
![]() for
some
for
some
![]() .
.
![]() is information about a set of situoids or situations
is information about a set of situoids or situations
![]() if
if
![]() for all
for all ![]() .
.![]() is also closed under
the rules (
is also closed under
the rules (![]() ), (
), (![]() ), (
), (![]() ) and (
) and (![]() ).
).![]() ,
written
,
written
![]() iff
iff
![]() for all situations
for all situations
![]() in
in ![]() . Then for any modal information frame
. Then for any modal information frame ![]() and any
propositions
and any
propositions ![]() and
and ![]() ,
,
![]() ,
,
![]() and
and
![]() are valid.
are valid.