



Next: Gesamtalgorithmus
Up: Partielle Korrektheit
Previous: Partielle Korrektheit
Um zu zeigen, daß der euklidische Algorithmus korrekt in ein Programm umgesetzt worden ist, reicht es zu zeigen,
daß die Invariante
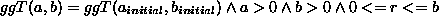
vor Beginn der Schleife, zu jedem Zeitpunkt in der Schleife und nach Beendigung der Schleife gilt.
Vor Beginn der Schleife gilt sie, sofern der Nutzer der Methode sich an die Vorbedingung
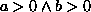
gehalten hat und der Funktion ein Wertepaar größer Null übergeben hat. Die vorher abgearbeitete Initialisierung
der lokalen Variablen führt zu einem Zustand, in dem gilt:
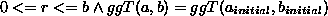
Verknüpft man diese beiden Bedingungen, die zu diesem Zeitpunkt selbstverständlich gelten müssen,
erhält man die Invariante
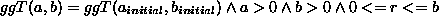
und hat somit gezeigt, daß sie bei korrekter Nutzung der Methode, sprich Einhaltung der Vorbedingung durch den Nutzer,
vor Beginn der Schleife gilt.
In der Schleife gilt sie offensichtlich zu jedem Zeitpunkt, da der euklidische Algorithmus korrekt umgesetzt wurde. Es
wird, wie in der Beschreibung des Algorithmus unter  verlangt, vor Beginn der Schleife der Variablen
verlangt, vor Beginn der Schleife der Variablen
 der Rest der Division von
der Rest der Division von  durch
durch 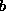 zugewiesen. Im weiteren wird, solange
zugewiesen. Im weiteren wird, solange  ungleich Null ist, der
Variablen
ungleich Null ist, der
Variablen  der Wert von
der Wert von 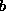 zugewiesen, der bisherige Divisor also zum Dividenden gemacht, und
zugewiesen, der bisherige Divisor also zum Dividenden gemacht, und 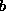 der Wert
von
der Wert
von  , der bisherige Rest also zum Divisor. Der neue Rest
, der bisherige Rest also zum Divisor. Der neue Rest  wird nun wiederum der Rest der Division von
wird nun wiederum der Rest der Division von  durch
durch 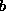 . Der euklidische Algorithmus wird also in allen Punkten umgesetzt und daher gilt auch hier die Invariante
. Der euklidische Algorithmus wird also in allen Punkten umgesetzt und daher gilt auch hier die Invariante
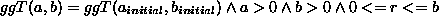
Auch nach der Beendigung der Schleife gilt die Invariante, da die Schleife bei Nullwerden des Restes  abbricht,
damit
abbricht,
damit
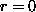
gilt, die Variablen  und
und 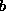 dabei jedoch immernoch größer als Null sein müssen, womit
dabei jedoch immernoch größer als Null sein müssen, womit
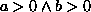
gilt und aufgrund der Eigenschaft des euklidischen Algorithmus
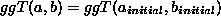
gelten muß. Die Verknüpfung aller drei zwangsläufig zutreffenden Bedingungen ergibt wieder die Invariante
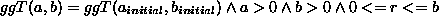
Durch Verknüpfung dieser mit der Negation der Schleifenbedingung ergibt sich
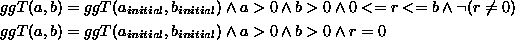
was die Nachbedingung darstellt. Da, wie oben gezeigt, der euklidische Algorithmus korrekt umgesetzt wurde, muß
hieraus nun folgen
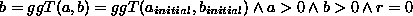




Next: Gesamtalgorithmus
Up: Partielle Korrektheit
Previous: Partielle Korrektheit
Michael Weiser
Fre Jan 7 00:42:53 CET 2000