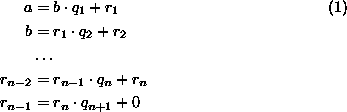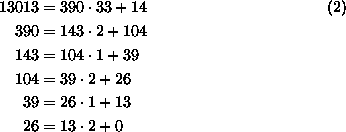Next: Berechnung des kgV
Up: Theoretische Grundlagen der Lösung
Previous: Theoretische Grundlagen der Lösung
[] definiert den größten gemeinsamen Teiler folgendermaßen:
Ist 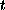 Teiler der natürlichen Zahlen
Teiler der natürlichen Zahlen 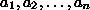 , so heißt
, so heißt 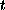 ein gemeinsamer Teiler dieser
Zahlen. Ein gemeinsamer Teiler
ein gemeinsamer Teiler dieser
Zahlen. Ein gemeinsamer Teiler 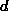 der Zahlen
der Zahlen 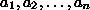 , der durch jeden der gemeinsamen Teiler dieser
Zahlen teilbar ist, heißt größter gemeinsamer Teiler (ggT) und wird mit
, der durch jeden der gemeinsamen Teiler dieser
Zahlen teilbar ist, heißt größter gemeinsamer Teiler (ggT) und wird mit 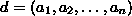 bezeichnet.
bezeichnet.
Beispiel:
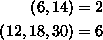
Zur Berechnung des größten gemeinsamen Teilers zweier natürlicher Zahlen
wird in diesem Projekt der euklidische Algorithmus verwendet. Dieser wird in []
folgendermaßen beschrieben:
Rechenverfahren, durch das der größte gemeinsame Teiler 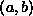 zweier positiver natürlicher Zahlen
zweier positiver natürlicher Zahlen
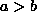
 durch schrittweise Division mit Rest bestimmt werden kann. Im ersten Schritt ist b Divisor, in jedem folgenden Schritt
wird der Divisior des vorhergehenden zum Dividenden gemacht und der Rest des vorhergehenden Schrittes zum Divisor. Da der
Rest
durch schrittweise Division mit Rest bestimmt werden kann. Im ersten Schritt ist b Divisor, in jedem folgenden Schritt
wird der Divisior des vorhergehenden zum Dividenden gemacht und der Rest des vorhergehenden Schrittes zum Divisor. Da der
Rest 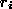 jedes Schrittes kleiner als der Divisor ist, bricht der e.A. nach endlich vielen Schritten mit dem Rest
jedes Schrittes kleiner als der Divisor ist, bricht der e.A. nach endlich vielen Schritten mit dem Rest
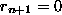 ab. Bezeichnet man die Quotienten mit
ab. Bezeichnet man die Quotienten mit 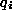 , so läßt sich das Ergebnis des e.A. durch
, so läßt sich das Ergebnis des e.A. durch
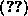 darstellen:
darstellen:
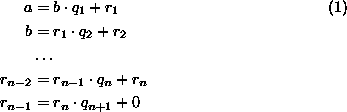
 als Beispiel:
als Beispiel:
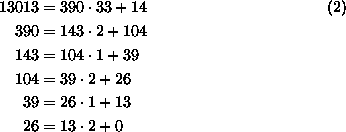
Setzt man nach der letzten Gleichung 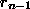 in die vorhergehende ein, so zeigt sich, daß
in die vorhergehende ein, so zeigt sich, daß 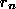 ein Teiler von
ein Teiler von
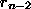 ist. Fährt man mit dem Rückwärtseinsetzen fort, so ergibt sich, daß
ist. Fährt man mit dem Rückwärtseinsetzen fort, so ergibt sich, daß 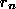 nach der 2. Gleichung
Teiler von
nach der 2. Gleichung
Teiler von 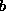 und nach der ersten Gleichung auch von
und nach der ersten Gleichung auch von  ist. Nach dieser ersten Gleichung muß jeder gemeinsame
Teiler von
ist. Nach dieser ersten Gleichung muß jeder gemeinsame
Teiler von  und
und 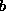 auch
auch  teilen, damit auch
teilen, damit auch 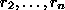 , d.h.
, d.h. 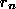 ist der größte
gemeinsame Teiler. Im Zahlenbeispiel
ist der größte
gemeinsame Teiler. Im Zahlenbeispiel 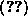 ist
ist 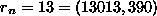 .
.




Next: Berechnung des kgV
Up: Theoretische Grundlagen der Lösung
Previous: Theoretische Grundlagen der Lösung
Michael Weiser
Fre Jan 7 00:42:53 CET 2000