Berechnung des kgV

Wiederum [] als Referenz herangezogen, definiert sich das kleinste gemeinsame Vielfache folgendermaßen:

Zu je natürlichen Zahlen gibt es genau eine natürliche Zahl v mit den Eigenschaften:

a.)

ist gemeinsames Vielfaches der 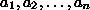, d.h. , , , .

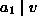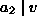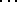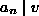b.)

ist 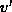irgendein gemeinsames Vielfaches der 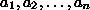, so ist Teiler von .

Man nennt das kleinste gemeinsame Vielfache (kgV) und bezeichnet es mit . [...] Für zwei beliebige ganze Zahlen gilt die Beziehung , die man für die Bestimmung des kleinsten gemeinsamen Vielfachen verwenden kann.

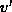Zur Berechnung des kleinsten gemeinsamen Vielfachen zweier natürlicher Zahlen kann also folgender Zusammenhang ausgenutzt werden:
 
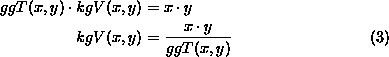
Multipliziert man zwei natürliche Zahlen, so muß das Ergebnis wiederum eine natürliche Zahl sein, die durch beide Faktoren teilbar ist. Teilt man dieses Produkt nun durch den größten gemeinsamen Teiler der beiden Zahlen, muß das Ergebnis wiederum eine natürliche Zahl sein, da der ggT Teiler beider Faktoren ist und somit auch Teiler des im vorigen ermittelten Produktes sein muß.