Der in der Klasse timetest implementierte unten als Ausschnitt angegebene Algorithmus ermittelte für verschiedene
als Referenz herangezogene günstige Zahlen die im folgenden Diagramm dargestellten Daten. Wie man sieht, bildet er
schlicht 
mal den ggT der anzugebenden Zahlen a und b. Um aussagekräftige Werte zu erhalten, wurde hier
als 
gewählt und konstant belassen.
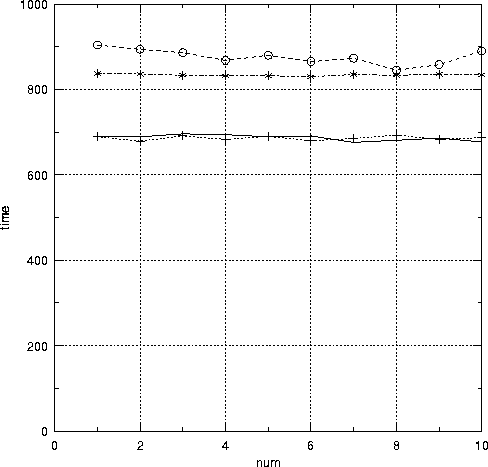
Das Diagramm zeigt vier Meßreihen, hervorgehoben durch die unterschiedliche Linien und Punktart. Auf der mit 'num'
beschrifteten x-Achse sind die gewählten Zahlen 
(und 
) abgetragen, für die der Algorithmus ausgeführt
wurde. Die mit 'time' bezeichnete y-Achse zeigt die für den kompletten Vorgang auf dem Beispielsystem
jeweils nötige Zeit in Millisekunden.
Die erste der unteren beiden Meßreihen, als durchgezogene Linie dargestellt, zeigt dabei die Laufzeit von
mal 
mit 
oder anders formuliert 
mit 
. Es wurden also die Zahlen
zwischen 
und 
je zehntausendmal auf sich selbst bearbeitet. Entsprechendes stellt die zweite gestrichelt
dargestellte Reihe dar, nur daß diesmal die Zahlen zwischen 
und 
verwendet wurden. Wie man
sieht, besteht kein signifikanter Unterschied zwischen beiden Meßreihen.
Die beiden oberen Kurven stellen dieselben beiden Zahlenbereiche dar, wobei jedoch 
jeweils als 
gewählt wurde, wodurch der Algorithmus nicht sofort terminieren kann, sondern erst einmal die Schleife aufrufen
und durchlaufen muß. Auffallend ist hierbei der recht große Offset zwischen unterer (
) und oberer
(
) Kurve. Doch erklärt sich die erhöhte Laufzeit bei größeren
Zahlen schnell durch die Verwendung der Klasse BigInteger zur Darstellung beliebig großer Zahlen. Diese arbeitet
intern mit Feldern, deren Größe der Anzahl der Stellen der Zahl entspricht. Bei größeren Zahlen wird
die Arithmetik dieser Klasse dann entsprechend langsamer. Das Nichtauftreten
eines entsprechenden Offsets in den ersten beiden Meßreihen erklärt sich durch den Wegfall von immerhin
drei Methodenaufrufen durch die komplette Nichtausführung der Schleife.
Es zeigt sich also, daß die Größe der Zahlen weitgehend unerheblich ist. Wichtiger ist hingegen ihre
Qualität hinsichtlich der Anzahl der Schleifendurchläufe, die nötig sind, bis der Divisionsrest 
wird. Im
Fall der ersten Meßreihe ist diese Null, während im zweiten die Schleife einmal durchlaufen werden muß.
Aufgrund des allgemeinen Zeitverhaltens des Algorithmus und der Verschiebung zwischen den Meßkurven liegt die
Vermutung nahe, daß der Algorithmus mit zunehmender Komplexität der Zahlen ein logarithmisches Laufzeitverhalten
an den Tag legen wird, wie bereits unter 
prinzipiell besprochen. Bei weiterer Annäherung an
den worst case wird die Laufzeit größer, zeigt jedoch weiterhin logarithmische Abhängigkeit von der
Komplexität der zu betrachtenden Zahlen.
Algorithmus:
