Next:
Einleitung
Vortrag Goedelscher Unvollstaendigkeitssatz
Einleitung
Vollstaendigkeitssatz
Sei
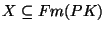. Dann sind folgende Beziehungen aequivalent:
(Vollstaendigkeitssatz v. Goedel) Fuer jede Menge X von Formeln,
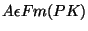gilt:
Beweis (2)
Beispiel Peano Arithmetik
Beschreibung der Wissensbasis (des abstrakten Modells) fuer natuerliche Zahlen
Goedelscher Unvollstaendigkeitssatz
Goedelisierung
Beweispaare
Substitution
Selbstbezueglichkeit nach Quine
Der endgueltige Satz
Folgerungen aus dem Satz
Moeglichkeiten, PA zu vervollstaendigen
Bedingungen fuer Unvollstaendigkeit
Schluss
About this document ...
Lee Chuck 2001-05-01
. Dann sind folgende Beziehungen
aequivalent:
gilt: